10. Electron Spin Resonance¶
10.1. Background¶
In 1925, two graduate students, Goudsmit and Uhlenbeck proposed the notion of electron spin, the spin angular momentum, \(S\), obeying the same quantization rules as those governing orbital angular momentum of atomic electrons. In particular, in any given direction, say the z-direction, the component, \(S_z\), is :
where \(m_s = \pm \frac{1}{2}\).
In addition the ‘spinning’ electron possesses a magnetic dipole moment, \(\vec{\mu}_s\), where
Here \(g\) is the Landé g-factor which is very close to 2 (actually 2.00232). As an exercise calculate the magnetic moment of an orbiting point charge and express it in terms of its angular momentum. If the electron is placed in a magnetic field, \(\vec{B}\), the magnetic moment will have the potential energy:
Combining equations (10.1), (10.2) and (10.3) one obtains:
Therefore, ignoring spin-orbit interactions, a given energy level for an atomic electron will be split due to spin into two levels, differing in energy by an amount of:
Electron Spin Resonance (ESR) refers to the situation where photons of a frequency \(f\) are absorbed or emitted during transitions between these two levels \(U_{+}\) and \(U_{-}\). By measuring \(f\) as a function of \(B\) and knowing the values of \(e\) and \(m_e\), the Landé g-factor can be determined. Using the relationship \(\Delta E = hf\) one obtains:
10.2. Experimental Details¶
The magnetic field is provided by a pair of Helmholtz coils in a series connection with an AC and a DC power supply (see Fig. 10.2). Thus the magnetic field has an average value, \(B_{av}\), given by the DC power supply and a superposed AC 60Hz component provided by the AC power supply. The resulting magnetic field \(B_H\) as a function of time is shown in Fig. 10.1:
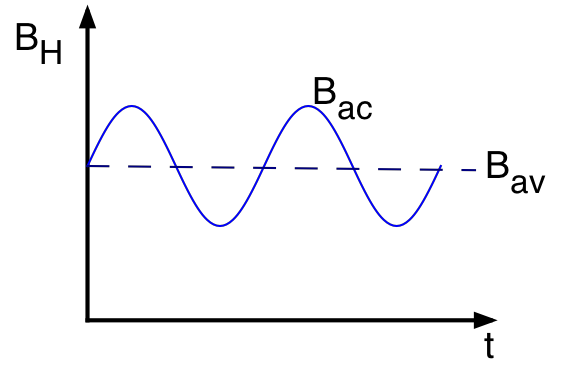
Fig. 10.1 Figure 1: The magnetic field at the center of the Helmholtz coils as a function of time.¶
The average magnetic field can be determined from the current \(I\) in the coil which is measured by the DC ammeter.

Fig. 10.2 Figure 2: Wiring of the Helmholtz coils using an AC and a DC power supply in series. The \(1\Omega\) resistor is used to determine the instantaneous coil current.¶
If the distance between the coils is equal to their radius \(R\), then midway between the coils and on their axis the magnetic field is given by:
where \(N_i\) is the number of turns in each coil. The AC voltage across the \(1\Omega\) resistor (see Fig. 10.2) is fed to the X-input of an oscilloscope. This causes the trace to sweep horizontally back and forth across the screen at 60 Hz in time with the alternating magnetic field. As the trace passes the center of the screen, we know that the corresponding magnetic induction is \(B_{av}\).
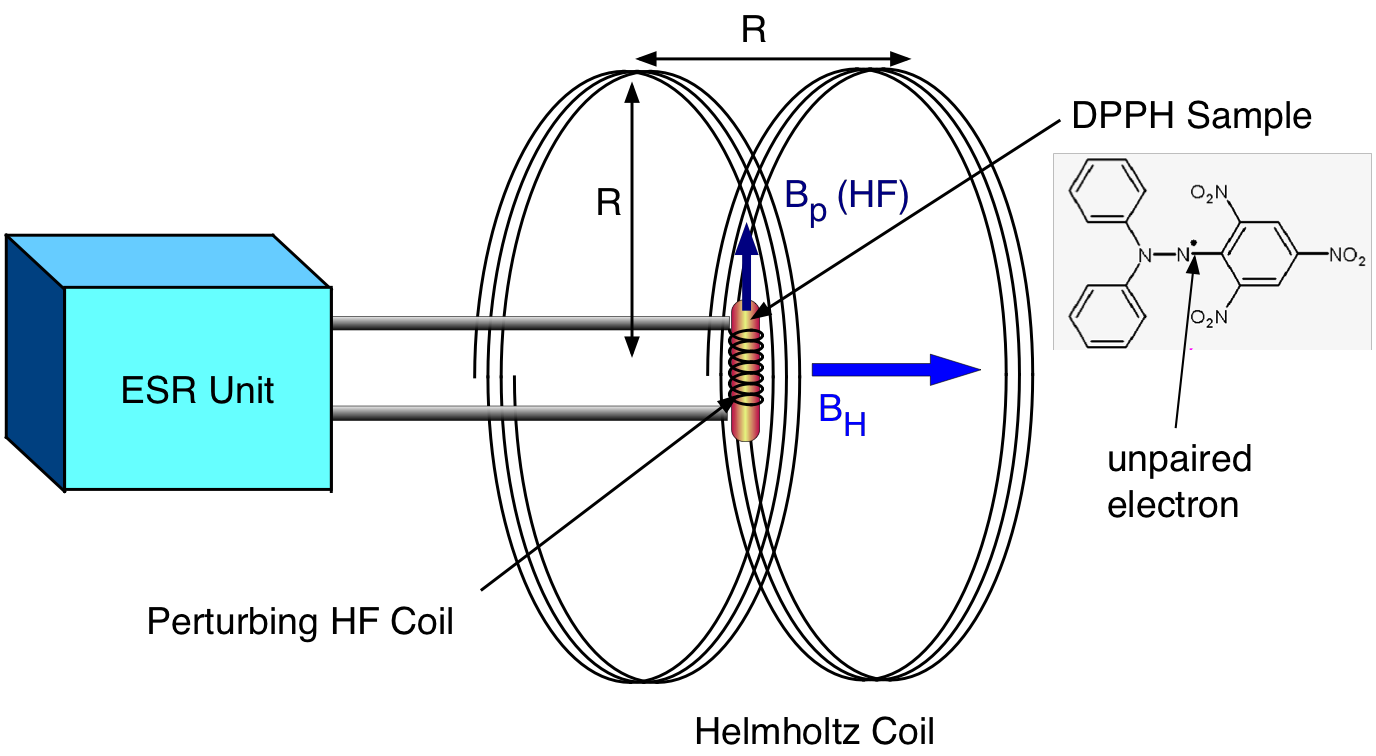
Fig. 10.3 Figure 3: ESR unit with DPPH sample, Helmholtz and signal (and perturbation) coils.¶
Electrons for this experiment are provided by a sample of diphenylpicrylhydrazyl (DPPH). An unpaired electron in this molecule moves on a highly delocalized orbit so that its orbital contribution to the magnetic moment is negligible. This electron can be viewed as essentially free, only its spin contributing to the magnetic moment. Thus the Landé g-factor for DPPH is very close to that for a free electron.
For the typical magnetic fields used in this experiment, photons of frequencies in the range ~25-50 MHz are required for the transitions referred to above. These are provided by a short coil connected to a high frequency oscillator. The magnetic field of this coil is perpendicular to that provided by the Helmholtz coils, an arrangement that results in a perturbing torque acting on the electron’s spin dipole moment. When the oscillator frequency matches the resonance condition, the impedance of the oscillator circuit decreases and the current increases. A DC voltage proportional to this current is fed to the Y-input of the oscilloscope.
10.3. Experimental Procedure¶
10.3.1. Connections¶
The Helmholtz coils have 320 turns each and a mean radius of 6.8 cm. Arrange the coils parallel to each other, as shown in Fig. 10.3, at a mean distance of 6.8 cm apart. The terminals should be pointing outwards. Arrange the ESR unit, also shown in Fig. 10.3, so that the small coil is accurately at the center of the Helmholtz coils. Place the glass tube containing the DPPH inside the small coil. Connect the Helmholtz coils in a series circuit with the AC and the DC power supplies , the ammeter and the resistor as shown in Fig. 10.2.
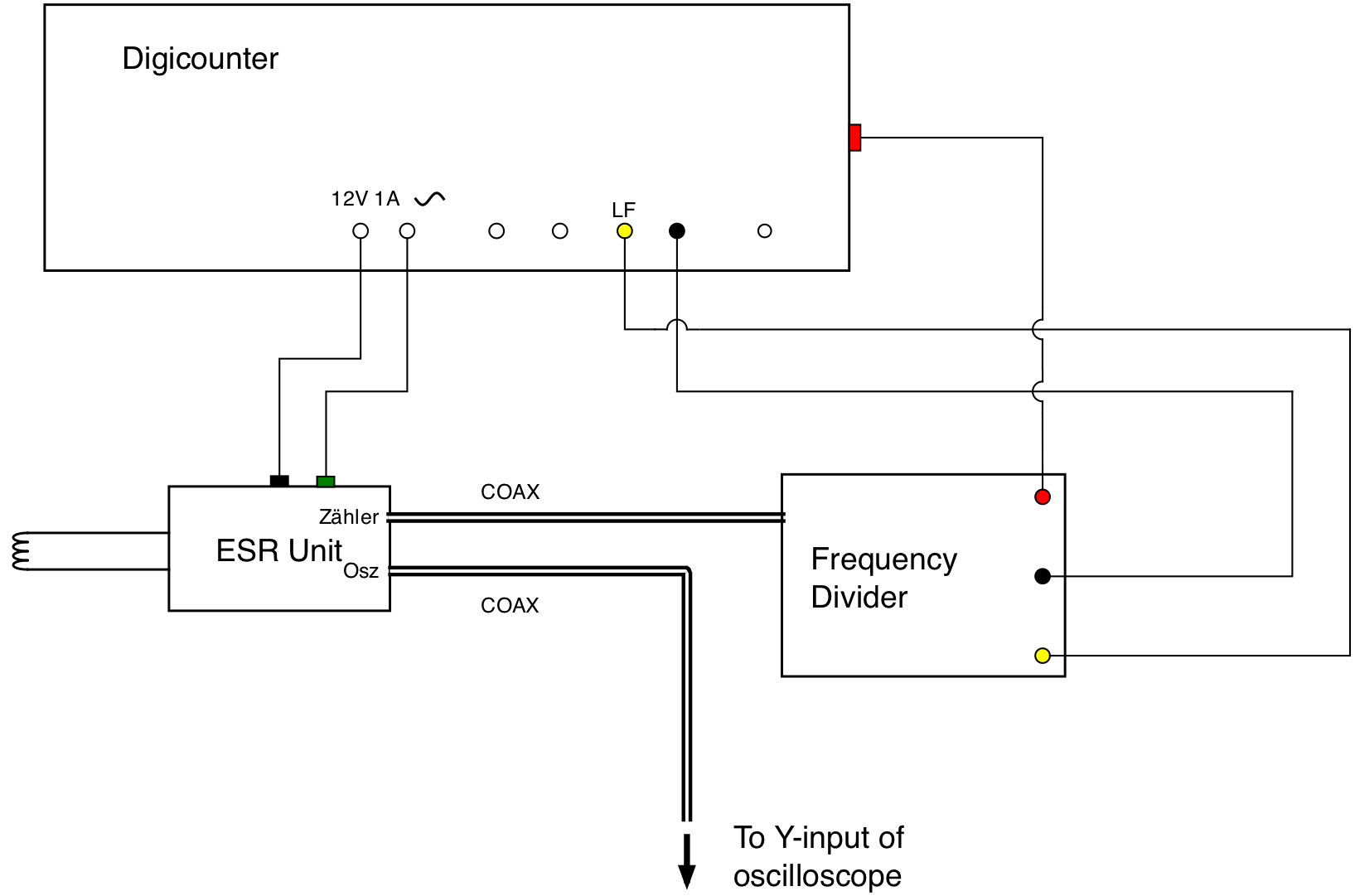
Fig. 10.4 Figure 4:Connection of the ESR signals and power supplies.¶
Use a coaxial cable to feed the voltage across the \(1\Omega\) resistor to the X-input of the oscilloscope. Connect the DIGICOUNTER, ESR unit and frequency divider as follows (see Fig. 10.4):
Connect the black middle socket of the frequency divider to the black FREQUENCY input socket of the DIGICOUNTER (2nd from right at the front).
Connect the yellow output socket of the frequency divider to the “lf” yellow FREQUENCY socket (3rd from right).
Connect the red power input socket of the frequency divider to the red 10 V output socket on the side panel of the DIGICOUNTER.
Connect the 12 V AC output of the DIGICOUNTER to the green and black input terminals on the ESR unit.
Connect the
Zähleroutput of the ESR unit to the “Input” of the frequency divider using a coaxial cable.Connect the
OSZoutput of the ESR unit to the Y-input of the oscilloscope, also using a coaxial cable.
On the DIGICOUNTER, set the FUNCTION switch to frequency, the
RANGE switch to kHz, slide the switch below FREQUENCY to the left
(to lf), set the single reading/continuous switch to
continuous. On the frequency divider, slide the switch to the
right (1/1000). Switch on the DIGICOUNTER and press RESET. The
DIGICOUNTER will now read the input frequency in MHz with the decimal
point in the correct position.
10.3.2. Setup and Measurements¶
Make sure that the direction of the magnetic fields produced by the two Helmholtz coils point in the same direction at the location of the sample.
Use the gauss meter and measure the magnetic field at the location of the sample as a function of the current in the coil. Compare your measurement to the calculated values from (10.7).
Set the X-gain on the oscilloscope to 0.1 V/cm and the coupling to DC. Using the horizontal positioning knob on the scope center the signal on the screen and adjust the AC power supply until the trace is about 8 cm wide.
Set the ESR frequency to its minimum value and then position the resonance peak in the center of the scope screen and adjust \(B_{av}\) via the DC power supply until the range in x is exactly symmetric around the center (see Fig. 10.4). Record the corresponding average coil current. Repeat this 2 to 3 times and record the result for each setting. By having the range of currents exactly centered around the resonance peak the magnetic field at the average current corresponds to the field where the resonance occurs.
Repeat the previous procedure for a total of 6 frequency settings, the last being the maximum obtainable. Record the corresponding DC current and determine the corresponding magnetic field. Since there should be a linear relationship between the frequency and the magnetic field, plot \(f\) as a function of \(B_{av}\) and fit a line. From the slope determine g. Include all errors and determine the uncertainty in g.
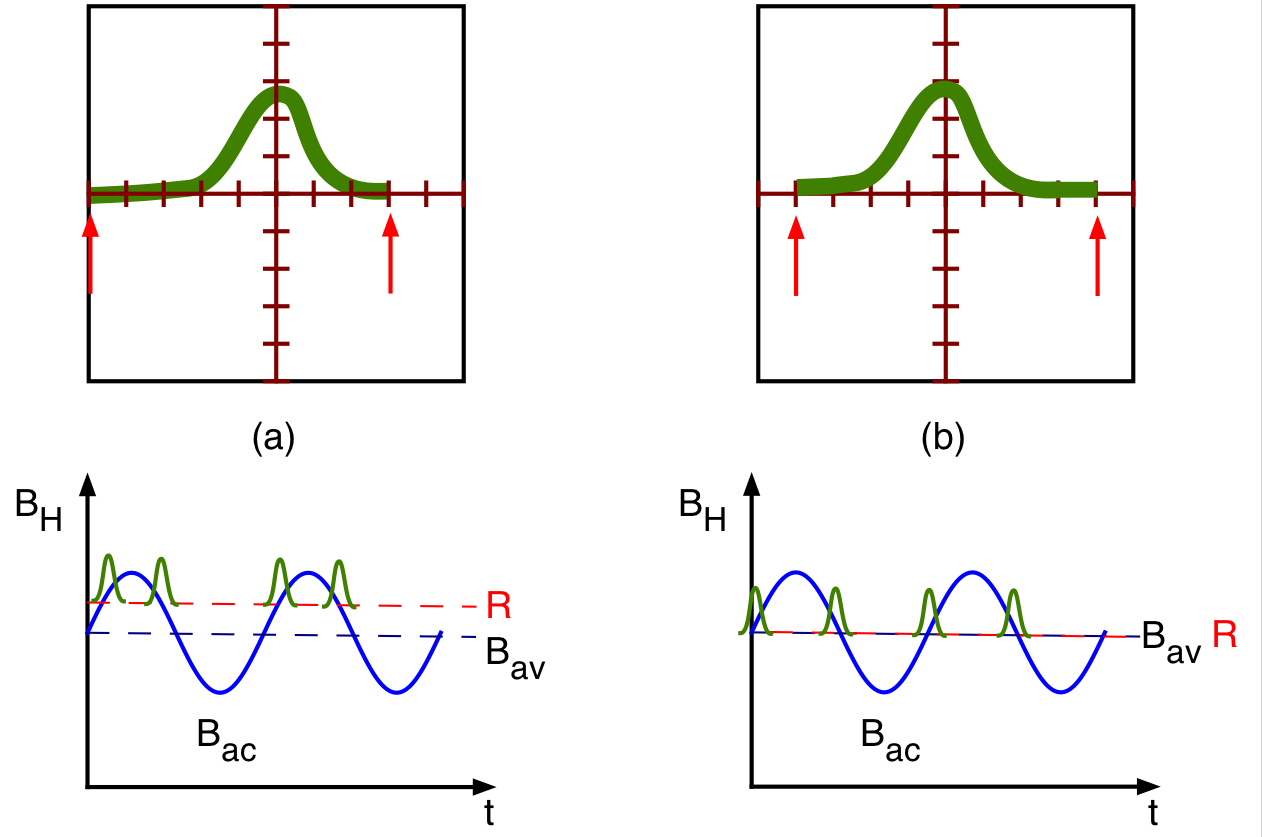
Fig. 10.5 Figure 5: Determining the coil current at which the ESR occurs using the current setup. (a) The current (or magnetic field) range is not centered around the ESR peak. The measured averaged DC current does not correspond the resonance field. (b) Range is centered and the resonance occurs at the average coil current. This is what you need¶